Gödel-Turing-Barrieren für mikroskopische Beschreibungen der makroskopischen Welt

Unten eine Computer unterstützte Übersetzung des Textes, die zwar vom Autor autorisiert ist, aber im Deutschen merkt man das.
Der englische Originalbeitrag hier.

Gödel-Turing-Barrieren
für mikroskopische Beschreibungen der
makroskopischen Welt

Im letzten Jahrzehnt gab es eine Fülle neuer Unentscheidbarkeitsresultate in der Physik, insbesondere auf dem Gebiet der Quantentheorie. Aus der Ferne betrachtet, können diese in zwei Kategorien von Entscheidungsproblemen unterteilt werden: solche, die über einen unbegrenzten Zeitbereich unvorhersehbar werden, und solche, bei denen räumlich begrenzte Bausteine, wenn sie zusammengesetzt werden, zu unentscheidbaren globalen Eigenschaften führen. Insbesondere die letztgenannte Klasse wirft die Frage auf, ob es eine fundamentale Barriere für mikroskopische Beschreibungen der makroskopischen Welt gibt, die letztlich auf die bahnbrechenden Arbeiten von Gödel [Göd31] und Turing [Tur36] zurückgehen.

In diesem Beitrag werden wir die reichhaltige Literatur der jüngsten Unentscheidbarkeitsresultate aus der Vogelperspektive betrachten. Anstatt auf die sehr unterschiedlichen physikalischen Details einzugehen, werden wir deren gemeinsame Grundlage untersuchen: eine Reduktion des Halteproblem, die durch Rückgriff auf den 2. Unvollständigkeitssatz von Gödel präzisiert werden kann und durch Berufung auf komplexitätstheoretische Argumente praktische Relevanz erhält. Wir werden robuste emergente makroskopische Effekte auf unberechenbaren Skalen diskutieren und uns am Ende ein leckeres Heißgetränk verdient haben.

Ein Rezept für unbeweisbare Sätze

Es gibt zwei Arten von mathematischen Unentscheidbarkeitsresultaten: solche, bei denen Unentscheidbarkeit im Sinne von Turing Unberechenbarkeit meint, und solche, bei denen sie im Sinne von Gödel Unbeweisbarkeit bedeutet. Fast alle Unentscheidbarkeitsresultate mit physikalischer Bedeutung basieren auf der Unberechenbarkeit des Turingschen Halteproblems. Wie wir jedoch ein paar Absätze weiter unten sehen werden, führen auch diese mit Hilfe des 2. Unvollständigkeitssatzes zu unbeweisbaren Aussagen.

Der direkte Weg von einem formalen System, wie ZFC, zu Unbeweisbarkeit mit einer physikalischen Interpretation scheint ohne Turings Maschinerie schwierig zu sein. Die bekannten mengentheoretischen forcing Techniken fügen ‘generische’ Mengen hinzu, die aus physikalischer Sicht schwer zu fassen sind. Einer der wenigen erwähnenswerten Versuche auf diesem direkten Weg ist in [dCDdB90, DD12] zu finden.

Im Folgenden werden wir uns aus sicherer Entfernung ansehen, wie aus dem Turingschen Halteproblem unbeweisbare Aussagen mit einer physikalischen Interpretation entstehen. Der erste und wichtigste Schritt dabei, ist eine Reduktion des Halteproblems. Im Prinzip könnte das Halteproblem durch jedes andere unentscheidbare Entscheidungsproblem ersetzt werden, aber in der Praxis scheint dies die einzig wirklich tragfähige Wurzel zu sein. Formal gesehen beginnen wir mit einer Teilmenge L ⊂ N, die nicht rekursiv ist, d.h. für die das Entscheidungsproblem “x ∈ L?” nicht berechenbar ist. Im Sprachgebrauch der theoretischen Informatik bezeichnet L eine Sprache, und die Standardwahl für L ist die Teilmenge der nummerierten Turing-Maschinen, die bei leerer Eingabezeichenkette anhalten. Das Kernstück eines jeden Turing-basierten Unentscheidbarkeits-Resultats ist dann eine berechenbare Abbildung, die zu jeder natürlichen Zahl x ∈ N eine logische Aussage S(x) in einem formalen System F zuordnet, das mit einer (in unserem Fall letztlich physikalischen) Interpretation ausgestattet ist, so dass

x ∈ L gilt, genau dann wenn S(x) wahr ist. (1)

Das heißt, es gibt einen physikalisch interpretierbaren Satz auf der rechten Seite von Gleichung(1), der sich auf berechenbare Weise auf eine Instanz x eines nicht berechenbaren Entscheidungsproblems bezieht. In den unten zusammengetragenen Resultaten und in den Referenzen ist jedes S(x) eine Aussage über ein individuelles physikalisches System, das durch x spezifiziert wird, wie “x hat eine spektrale Lücke”, “x thermalisiert”, “x erreicht einen Zustand mit einer bestimmten Eigenschaft”, usw..
Die Abbildung x → S(x) ist natürlich der Teil, der die meiste Arbeit macht und an dem sich die Fülle von Ergebnissen in verschiedene Richtungen verzweigt.
Bevor wir uns diese Abbildung genauer ansehen, betrachten wir die Implikationen von Gleichung (1) hinsichtlich Beweisbarkeit. Zu diesem Zweck nehmen wir an, dass das formale System F effektiv axiomatisiert ist. Das bedeutet, dass syntaktische Korrektheit, Zugehörigkeit zur Menge der Axiome und die Gültigkeit eines Beweises algorithmisch entscheidbar sein sollen. Daraus ergibt sich, dass es prinzipiell möglich ist, alle beweisbaren Sätze von F rekursiv aufzuzählen, indem man alle potentiellen Beweise zunehmender Länge durchläuft und dabei ungültige eliminiert. Wir nehmen auch an, dass F logisch korrekt ist, d. h., dass alles, was in F beweisbar ist, wahr ist. Nehmen wir nun an, dass für alle (außer endlich viele) x entweder S(x) oder die Negation ¬S(x) in F beweisbar wäre. Da wir dann rekursiv alle Theoreme in F aufzählen könnten, gäbe es einen Algorithmus, der “x ∈ L?” entscheidet – im Widerspruch zu unserer Wahl von L. Definieren wir als S die Menge aller S(x), erhalten wir also:

S enthält unendlich viele Sätze, die in F nicht beweisbar sind. (2)

Die unspezifische Unendlichkeit in (2) ist im Grunde der Preis, den man für den Rückgriff auf die Berechenbarkeitstheorie zahlt – schließlich sind endliche Entscheidungsprobleme immer entscheidbar. Unter Berufung auf den 2. Unvollständigkeitssatz von Gödel kann man jedoch im Prinzip, einen bestimmten unbeweisbaren Satz in S identifizieren, wenn L tatsächlich die Menge der haltenden Turing-Maschinen ist. Betrachten wir zu diesem Zweck eine Turing-Maschine, die eine Schleife über alle beweisbaren Sätze von F durchläuft und anhält, wenn sie eine Inkonsistenz gefunden hat. Sei x = c die Nummer einer solchen Turingmaschine. Dann ist c ∈ L, wenn und nur wenn F nicht konsistent ist. Da letzteres bei einem logisch korrekten und damit konsistenten F aufgrund des 2. Unvollständigkeitssatzes von Gödel nicht bewiesen werden kann (wobei stillschweigend angenommen wird, dass F groß genug ist), erhalten wir, dass

S(c) in F nicht beweisbar ist. (3)

In [YA16] wurde eine explizite Turing-Maschine mit 7910 Zuständen konstruiert, die anhält wenn, und nur wenn, ZFC inkonsistent ist. Unter einer geeigneten Abbildung c → S(c) führt dies dann auf einen expliziten Satz, der in ZFC unbeweisbar ist. Dieses Argument wurde in [Cub21] für den Fall dargelegt, dass jedes S(x) eine Aussage über eine Spektrallücke eines Quantenspinsystems ist, aber es gilt ebenso für alle anderen unentscheidbaren Ergebnisse, die aus dem Halteproblem hervorgehen. Und davon gibt es viele …¹

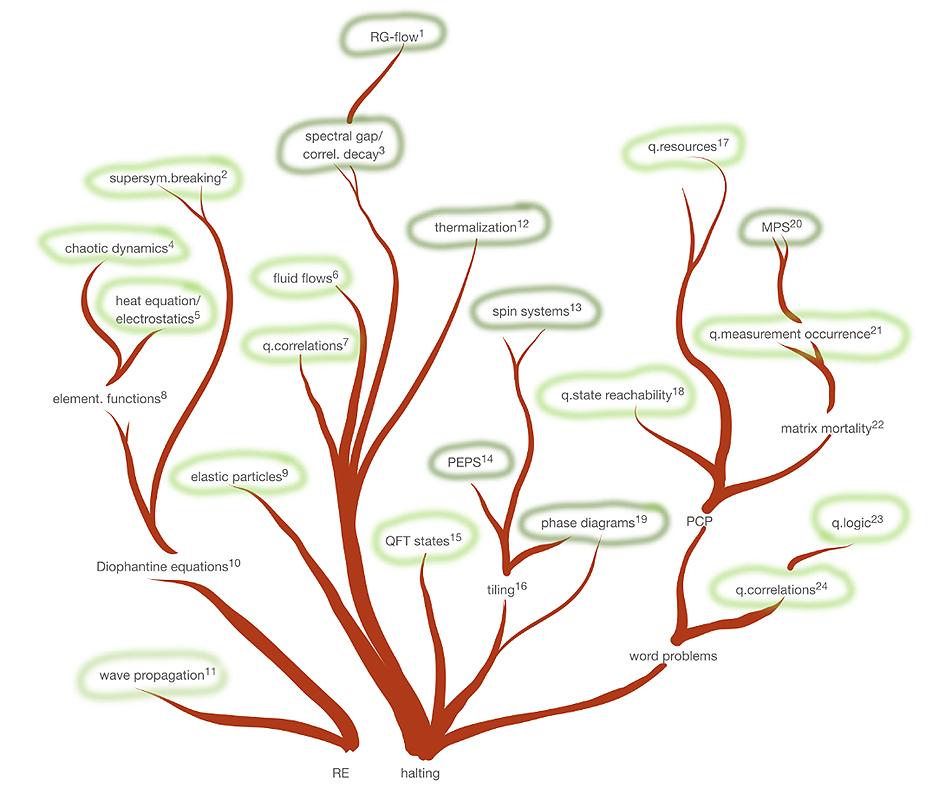
Abbildung 1: Der Baum der unentscheidbaren Probleme. Jeder Zweig verbindet zwei Klassen von Problemen eines Reduktionsarguments, das die Unentscheidbarkeit des weiter oben liegenden Problems beweist. Entscheidungsprobleme mit physikalischer Interpretation sind grün dargestellt. Dunkleres Grün kennzeichnet Probleme, die nach makroskopischen Eigenschaften von mikroskopisch gegebenen Systemen fragen. “q.” steht für Quanten. Die Referenzen sind in der Fußnote aufgeführt.¹

Der Unentscheidbarkeits-Baum

Das Halteproblem ist die Wurzel fast aller beweisbar “unentscheidbaren” Probleme denen eine physikalische Interpretation zu Grunde liegt. Die Reduktion des Halteproblems erfolgt jedoch in der Regel nicht in einem Schritt (und wenn doch, kann dieser “Schritt” leicht Dutzenden oder einhundert Seiten umfassen, wie in [CPGW22] oder [JNV+20]). Typischerweise sieht die Abbildung L → S eher wie L → A → B → . . . → S aus, wohinter sich eine Kette von Reduktionsschritten verbirgt. Auf diese Weise erhält die Menge der vorhandenen Ergebnisse die Struktur eines Baumes mit den physikalisch interpretierbaren Unentscheidbarkeitsergebnissen an den Blättern oder äußeren Ästen. Die zugrundeliegende Wurzel ist das Halteproblem oder, allgemeiner, die Menge RE der rekursiv aufzählbaren Sprachen, von denen das Halteproblem das “härteste” ist, wenn man es als Entscheidungsproblem betrachtet. In den Worten der Komplexitätstheorie ist das Halteproblem RE-vollständig.

Weiter oben hat der Baum der unentscheidbaren Probleme einige markante Äste, von denen drei besonders hervorstechen, da sie häufig als Zwischenschritte zur Reduktion verwendet werden:

Diophantische Gleichungen: Dies sind Polynomgleichungen in mehreren ganzzahlig wertigen Variablen – wie die Gleichungen in Fermats letztem Satz. Ein bemerkenswertes Theorem von Matiyasevich [Mat70], Davis, Putnam und Robinson [DPR61] zeigt, dass RE mit der Klasse der diophantischen Mengen identifiziert werden kann, die Projektionen der Lösungsmengen diophantischer Gleichungen sind.
Wortprobleme: diese existieren für Gruppen, Halbgruppen, (Semi-)Thue-Systeme und andere Strukturen. Ihr gemeinsames Merkmal ist die Frage, ob zwei Wörter, die aus einem gegebenen Alphabet gebildet werden, die gleiche “Bedeutung” haben, d.h. in dieselbe Äquivalenzklasse fallen. Eine besonders oft verwendete Problemklasse dieser Art ist das Post’sche Korrespondenzproblem (PCP).
Bei Kachelproblemen wird gefragt, ob es möglich ist, die Ebene mit einer bestimmten Menge von Kacheln und Regeln für deren Anordnung zu kacheln.

Der Baum der unentscheidbaren Probleme ist in Abb.1 dargestellt. Es ist unnötig zu erwähnen, dass es verschiedene Formen von Willkür in dieser Abbildung gibt, und wie bei jedem Bild eines gesunden Baumes sind nicht alle Blätter sichtbar.

Der Unentscheidbarkeits-Baum hat harte endliche Wurzeln

Wie sollen wir die Fülle der “physikalisch interpretierbaren” Unentscheidbarkeits- Ergebnisse interpretieren? Bleibt irgendetwas von Bedeutung, wenn wir einige Schichten der Idealisierung entfernen? Eine zentrale und kritisierbare Annahme ist immer eine Form von Unendlichkeit, die in jeder der Problemstellungen auftaucht: unendliche räumliche Ausdehnung, unendliche zeitliche Ausdehnung oder unendliche Präzision (oder mehr als eine davon). Klettern wir den Baum hinab, finden wir die Wurzel dieser Unendlichkeiten in der unbeschränkten Laufzeit der Turing-Maschine – eine Annahme, die für das Argument notwendig zu sein scheint. Was also, wenn wir diese Unendlichkeiten durch etwas Endliches ersetzen?

Dann werden die betrachteten Probleme zwar prinzipiell entscheidbar, aber es gibt gute Gründe für die Annahme, dass viele von ihnen in der Praxis unentscheidbar bleiben:

Die zeitbeschränkte Version des Halteproblems für (nichtdeterministische) Turing-Maschinen ist eines der Paradebeispiele für die schwierigsten Probleme innerhalb der berüchtigten Komplexitätsklasse NP, d.h. es ist NP-vollständig.² Wenn also die Reduktionen entlang der Äste und Zweige effizient berechenbar sind (was typischerweise der Fall ist), dann erbt das physikalisch interpretierbare Problem weiter oben im Baum die Schwierigkeit der Wurzel. Mit anderen Worten: Während die endlichen Analoga der Aussagen in S beweisbar werden, wird das Finden ihrer Beweise praktisch unlösbar bleiben (es sei denn, es gibt einen unerwarteten Kollaps in der Komplexitätstheorie). Eine detailliertere Ausarbeitung dieses Gedankenganges findet sich in [KvdES+22].

Wir können jedoch noch einen Schritt weiter gehen und eine weitere potenzielle Unzulänglichkeit dieses Arguments beleuchten: Schließlich ist NP-Vollständigkeit ein worst-case Konzept, was nicht notwendigerweise bedeutet, dass Instanzen des betrachteten Problems im Durchschnitt oder typischerweise schwer sind. Zum Beispiel benötigt das Hamiltonsche-Pfad Problem, obwohl es NP-vollständig ist, im Durchschnitt nur lineare Zeit [GS87]. In ähnlicher Weise ist das Knapsack-Problem NP-vollständig, aber in der Praxis gut handhabbar [Sha82].

Dagegen scheinen die Wurzeln des Unentscheidbarkeitsbaums, wenn man sie auf eine endliche Länge stutzt, auf eine robustere Weise schwer zu sein – sie scheinen alle im Durchschnitt NP–schwer zu sein. Dies wurde für die beschränkten Versionen des Halte- und des Kachelproblems [Lev86], für Wortprobleme für Gruppen [Wan95], Thue-Systeme [WB95] und PCP [Gur91] bewiesen und für diophantische Probleme in [VR92] diskutiert. In jüngerer Zeit wurde sogar gezeigt, dass die beschränkte Version des Halteproblems stark generisch NP-vollständig ist [MU16].

Über die Analyse der worst-case-Komplexität hinaus erweisen sich Reduktionen als wesentlich subtiler und schwieriger zu beweisen. Daher gelten die oben erwähnten Ergebnisse für den Durchschnittsfall nicht automatisch und ohne weiteres weiter oben im Baum. Die Wurzeln scheinen jedoch aus besonders schwierigen Problemen zu bestehen, selbst wenn sie auf endliche Länge gekürzt werden und es wäre seltsam, wenn sich nicht auch etwas davon in den Blättern widerspiegeln würde.

Emergente Effekte auf nicht berechenbaren Skalen

Es ist nun an der Zeit, sich der Frage zuzuwenden, inwieweit die oben diskutierten Ergebnisse ein Hindernis für die Ableitung makroskopischer Phänomene aus mikroskopischen Gesetzen sind. Mit anderen Worten, auf welche Art von Emergenz deuten sie hin?

In dieser Diskussion werden wir uns auf diejenigen Unentscheidbarkeitsergebnisse konzentrieren, die sich mit einem solchen räumlichen (und nicht mit einem zeitlichen) Problem befassen. Das Problem der spektralen Lücke, das in [CPGW22, CPGW15, BCLPG20, Cub21] für Quanten-Spin-Gitter mit lokalen, translationsinvarianten Wechselwirkungen untersucht wurde, ist eines dieser Beispiele.

Unentscheidbarkeitsergebnisse dieser Art zeigen makroskopische Phänomene, die sich nur dann aus mikroskopischen Gesetzen ableiten lassen, wenn die Beobachtungsskala im Voraus festgelegt (oder begrenzt) wird. Wenn wir jedoch fragen: “Gibt es eine Skala, auf der das Phänomen auftritt?”, können die mikroskopischen Gesetze grundsätzlich unzureichend für eine Antwort sein. Noch wichtiger ist, dass die Unterscheidung zwischen dem begrenzten und dem unbeschränkten Fall praktisch verschwindet, wenn wir komplexitätstheoretische Annahmen heranziehen (wie P ̸ = NP oder sein Gegenstück AvgP ̸ = DistNP), unter denen “in der Praxis unlösbar” in “im Prinzip unlösbar” übergeht.

In diesem Zusammenhang ist es erwähnenswert, dass die Unentscheidbarkeit der spektralen Lücke gut mit der notorischen Schwierigkeit dieses Problems übereinstimmt, mit der praktizierende mathematische Physiker selbst bei den einfachsten physikalischen Modellen konfrontiert sind. Nehmen wir zum Beispiel das antiferromagnetische Spin-1 1D-Heisenberg-Modell. In diesem Fall wird die Wechselwirkung zwischen benachbarten Spins durch eine 9 × 9-Matrix beschrieben, die nur 12 von Null verschiedene Einträge enthält, die alle +- 1 sind. Die Vermutung, dass ein Quantensystem von Spins, das auf diese Weise auf einer Spin-Kette wechselwirkt, eine spektrale Lücke besitzt, ist als Haldane Vermutung [Hal83, LWMA17] bekannt geworden. Trotz der eklatanten Einfachheit des Modells ist ein Beweis dieser Vermutung auch nach 40 Jahren nicht in Sicht. Der numerische Beweis für diese Vermutung beschränkt sich derzeit auf Systeme mit einigen hundert Spins. Was aber, wenn es 10^5 oder 10^10 sind? Die Unentscheidbarkeitsergebnisse zeigen, dass Extrapolationen von kleineren auf größere Skalen unzuverlässig sein können, unabhängig davon, wie groß die “kleinen” Skalen waren. Dass selbst relativ einfache Systeme ihre Eigenschaften auf beliebig (und im Allgemeinen unberechenbar) großen Skalen abrupt ändern können, wurde in [BCL+18] gezeigt.

Die skalengetriebenen Phasenübergänge in [BCL+18] zeigen eine drastische Änderung der niederenergetischen Eigenschaften eines 2D-Quantenspinmodells: unterhalb einer Gittergröße N ist der Grundzustand vollständig klassisch und durch eine konstante spektrale Lücke getrennt.

Oberhalb von N weist der Niederenergiesektor jedoch extreme Quanteneigenschaften auf. Entscheidend ist, dass es im Allgemeinen unentscheidbar ist, ob ein solches N existiert, und dass es selbst für relativ einfache Systeme astronomisch groß sein kann (N > 10^36534 für Spindimensionen ≤ 10 in den Beispielen von [BCL+18]).

In der Diskussion über Emergenz und Reduktionismus wird oft die Frage gestellt, ob Gesetze auf höherer Ebene aus Gesetzen auf niedriger Ebene abgeleitet werden können. Die Konsequenz aus den diskutierten Unentscheidbarkeitsergebnisse ist jedoch, dass es in diesen Fällen keine Gesetze auf höherer Ebene gibt. Angenommen, es gäbe sie: Dann könnten wir sie zu unserem formalen System hinzufügen und genau dasselbe Argument wiederholen – Turings Halteproblem wäre immer noch unentscheidbar und der 2. Unvollständigkeitssatz von Gödel wäre immer noch gültig.³ Darüber hinaus wird sich dieses Bild, abhängig von komplexitätstheoretischen Annahmen, nicht ändern, wenn wir die Beobachtungsskala begrenzen: In einigen Fällen ist die einzige Möglichkeit, herauszufinden, ob ein bestimmtes Phänomen auf einer Skala von Interesse auftritt, die vollständige Berechnung oder Simulation bis zu dieser Größenordnung. Es gibt keine verlässliche Heuristik, keine übergeordnete Gesetzmäßigkeit – keine Abkürzung!

Und wenn Sie das Ende dieses Textes nicht über eine Abkürzung, sondern „auf die harte Tour“ erreicht haben, dann haben Sie sich wahrlich ein leckeres heißes Getränk verdient. Genießen Sie es …

——————————————

1 Abb. 1 zeigt die Beziehung zwischen den folgenden Referenzen: 1[WOC22], 2[Tac22], 3[CPGW22, CPGW15, BCLPG20], 4[dCD91], 5[CCSS94], 6[Tao19, CMPSP21], 7[JNV+20], 8[Ric68, Wan74], 9[FT82, Moo90, Moo91], 10[Mat70, DPR61], 11[PER81], 12[SM21], 13[Kan90], 14[SMG+20], 15[Kom64], 16[Wan61, Ber66, Rob71], 17[SS21], 18[WCPG11], 19[BCW21], 20[KGE14, DlCCC+16], 21[EMG12], 22[CHHN14], 23[Fri21], 24[Slo20]

2 Tatsächlich ist sie sogar EXP-vollständig, wenn binär und nicht

unär kodiert wird. Allerdings ist es schwieriger, diese Eigenschaft bei Reduktionen zu erhalten.

3 Dies setzt natürlich voraus, dass wir auf realistischem Boden bleiben und uns von nicht-rekursiven axiomatischen Systemen und Hypercomputern fern halten.

Literaturliste

[BCL⁺18]	–	Johannes Bausch, Toby S Cubitt, Angelo Lucia, David Perez-Garcia, and Michael M Wolf. Size-driven quantum phase transitions. Proceedings of the National Academy of Sciences, 115(1):19–23, 2018.
[BCLPG20]		Johannes Bausch, Toby S. Cubitt, Angelo Lucia, and David Perez- Garcia. Undecidability of the spectral gap in one dimension. Physical Review X, 10(3):031038, 2020.
[BCW21]		Johannes Bausch, Toby S. Cubitt, and James D. Watson. Uncomputability of phase diagrams. Nature Communications, 12(1):452, Jan 2021.
[Ber66]		R. Berger. The Undecidability of the Domino Problem. Memoirs ; No 1/66. American Mathematical Society, 1966.
[CCSS94]		Cristian Calude, Douglas I. Campbell, Karl Svozil, and Doru Stefanescu. Strong determinism versus computability. In The Foundational Debate. Complexity and Constructivity in Mathematics and Physics. Vienna Circle Institute Yearbook, Vol. 3, ed. by Werner DePauli Schimanovich, Eckehart Koehler and Friedrich Stadler. Kluwer, Dordrecht, Boston, London, 1995, p.115-131, pages 115–131, 1994, quant-ph/9412004.
[CHHN14]		Julien Cassaigne, Vesa Halava, Tero Harju, and Fran¸cois Nicolas. Tighter undecidability bounds for matrix mortality, zero-in-the-corner problems, and more. CoRR, 2014, 1404.0644. arxiv:1404.0644.
[CMPSP21]		Robert Cardona, Eva Miranda, Daniel Peralta-Salas, and Francisco Presas. Constructing turing complete euler flows in dimension 3. Proceedings of the National Academy of Sciences, 118(19):e2026818118, 2021.
[CPGW15]		Toby S. Cubitt, David Perez-Garcia, and Michael M. Wolf. Undecidability of the spectral gap. Nature, 528:207, December 2015.
[CPGW22]		Toby Cubitt, David Perez-Garcia, and Michael M. Wolf. Undecidability of the spectral gap. Forum of Mathematics, Pi, 10:e14, 2022.
[Cub21]		Toby S. Cubitt. A note on the second spectral gap incompleteness theorem, 2021. arXiv:2105.09854.
[dCD91]		N. C. A. da Costa and F. A. Doria. Undecidability and incompleteness in classical mechanics. International Journal of Theoretical Physics, 30(8):1041–1073, 1991.
[dCDdB90]		N. C. A. da Costa, F. A. Doria, and J. A. de Barros. A suppes predicate for general relativity and set-theoretically generic spacetimes. International Journal of Theoretical Physics, 29(9):935–961, Sep 1990.
[DD12]		Francisco Antonio Doria and Manuel Doria. Einstein meets Gödel. New Mathematics and Natural Computation, 08(01):123–137, 2012.
[DlCCC⁺16]		G. De las Cuevas, T. S. Cubitt, J. I. Cirac, M. M. Wolf, and D. Pérez- Garcia. Fundamental limitations in the purifications of tensor networks. Journal of Mathematical Physics, 57(7), 2016.
[DPR61]		Martin Davis, Hilary Putnam, and Julia Robinson. The decision problem for exponential diophantine equations. Annals of Mathematics, 74(3):425–436, 1961.
[EMG12]		J. Eisert, M. P. Müller, and C. Gogolin. Quantum measurement occur rence is undecidable. Phys. Rev. Lett., 108:260501, Jun 2012.
[Fri21]		Tobias Fritz. Quantum logic is undecidable. Archive for Mathematical Logic, 60(3):329–341, May 2021.
[FT82]		Edward Fredkin and Tommaso Toffoli. Conservative logic. International Journal of Theoretical Physics, 21(3):219–253, 1982.
[God31]		Kurt Godel. Über formal unentscheidbare sätze der principia mathematica und verwandter Systeme i. Monatshefte für Mathematik und Physik, 38(1):173–198, Dec 1931.
[GS87]		Yuri Gurevich and Saharon Shelah. Expected computation time for hamiltonian path problem. SIAM Journal on Computing, 16(3):486– 502, 1987.
[Gur91]		Yuri Gurevich. Average case completeness. Journal of Computer and System Sciences, 42(3):346–398, 1991.
[Hal83]		F. D. M. Haldane. Nonlinear field theory of large-spin heisenberg anti- ferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis néel state. Phys. Rev. Lett., 50:1153–1156, Apr 1983.
[JNV⁺20]		Zhengfeng Ji, Anand Natarajan, Thomas Vidick, John Wright, and Henry Yuen. MIP^∗= RE. 2020. arXiv:2001.04383.
[Kan90]		I. Kanter. Undecidability principle and the uncertainty principle even for classical systems. Phys. Rev. Lett., 64:332–335, Jan 1990.
[KGE14]		M. Kliesch, D. Gross, and J. Eisert. Matrix-product operators and states: Np-hardness and undecidability. Phys. Rev. Lett., 113:160503, Oct 2014.
[Kom64]		Arthur Komar. Undecidability of macroscopically distinguishable states in quantum field theory. Phys. Rev., 133:B542–B544, Jan 1964.
[KvdES⁺22]		Andreas Klingler, Mirte van der Eyden, Sebastian Stengele, Tobias Rein- hart, and Gemma De las Cuevas. Many bounded versions of undecidable problems are np-hard, 2022. arxiv.2211.13532.
[Lev86]		Leonid A Levin. Average case complete problems. SIAM Journal on Computing, 15(1):285–286, 1986.
[LWMA17]		Miklós Lajkó, Kyle Wamer, Frédéric Mila, and Ian Affleck. Generalization of the haldane conjecture to su(3) chains. Nuclear Physics B, 924:508–577, 2017.
[Mat70]		Yuri Vladimirovich Matiyasevich. The diophantineness of enumerable sets. In Doklady Akademii Nauk, volume 191, pages 279–282. Russian Academy of Sciences, 1970.
[Moo90]		Cristopher Moore. Unpredictability and undecidability in dynamical systems. Phys. Rev. Lett., 64:2354–2357, May 1990.
[Moo91]		C Moore. Generalized shifts: unpredictability and undecidability in dynamical systems. Nonlinearity, 4(2):199, 1991.
[MU16]		Alexei Miasnikov and Alexander Ushakov. Generic case completeness. Journal of Computer and System Sciences, 82(8):1268–1282, 2016.
[PER81]		Marian Boykan Pour-El and Ian Richards. The wave equation with computable initial data such that its unique solution is not computable. Advances in Mathematics, 39(3):215 – 239, 1981.
[Ric68]		Daniel Richardson. Some undecidable problems involving elementary functions of a real variable. Journal of Symbolic Logic, 33(4):514–520, 1968.
[Rob71]		Raphael M. Robinson. Undecidability and nonperiodicity for tilings of the plane. Inventiones mathematicae, 12(3):177–209, 1971.
[Sha82]		Adi Shamir. A polynomial time algorithm for breaking the basic merkle- hellman cryptosystem. In 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), pages 145–152, 1982.
[Slo20]		William Slofstra. Tsirelson’s problem and an embedding theorem for groups arising from non-local games. Journal of the American Mathematical Society, 33(1):1–56, 2020.
[SM21]		Naoto Shiraishi and Keiji Matsumoto. Undecidability in quantum thermalization. Nature Communications, 12(1):5084, Aug 2021.
[SMG⁺20]		G Scarpa, András Molnár, Yimin Ge, Juan José García-Ripoll, Norbert Schuch, David Pérez-García, and S Iblisdir. Projected entangled pair states: Fundamental analytical and numerical limitations. Physical Review Letters, 125(21):210504, 2020.
[SS21]		Matteo Scandi and Jacopo Surace. Undecidability in resource theory: Can you tell resource theories apart? Phys. Rev. Lett., 127:270501, Dec 2021.
[Tac22]		Yuji Tachikawa. Undecidable problems in quantum field theory, 2022. arxiv.2203.16689.
[Tao19]		Terence Tao. On the universality of the incompressible Euler equation on compact manifolds, II. Non-rigidity of Euler flows. arXiv preprint arXiv:1902.06313, 2019.
[Tur36]		Alan Turing. On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society, 42(1):230–265, 1936.
[VR92]		Ramarathnam Venkatesan and Sivaramakrishnan Rajagopalan. Average case intractability of matrix and diophantine problems. In Proceedings of the twenty-fourth annual ACM symposium on Theory of Computing, pages 632–642, 1992.
[Wan61]		H. Wang. Proving theorems by pattern recognition – ii. The Bell System Technical Journal, 40(1):1–41, Jan 1961.
[Wan74]		Paul S. Wang. The undecidability of the existence of zeros of real elementary functions. J. ACM, 21(4):586–589, October 1974.
[Wan95]		Jie Wang. Average-case completeness of a word problem for groups. In Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, STOC ’95, page 325–334, New York, NY, USA, 1995. Association for Computing Machinery.